Language Processing Regular Expression
Compiler
- gcc is compiler. series of components
- compiler is simply a program
- can be hand-coded
- compilers/translators are built mechanically from grammars
- specification is the key
- grammar: set of rules specifying a language: formal purpose of a compiler
- language translation
- source language to target language images -source and target programs should be “equivalent”
- often high level language to machine language
- any combinations of languages is possible
- think of it also as a function/mapping between the languages
source -> compiler -> target
c -> gcc -> assembly/ml
- scanner
- group characters into tokens
- lexical analysis
- determine meaningful chunks
- integer-literal
- float-literal
- string
- identifier
- relational-operator
- group characters into tokens
- parser
- group tokens into constructs
- codegenerator
- translate source constructs to target
Regular Expression
. concatenation [ implicit by writing two symbols next to each other ] | choice
- kleene star; repetition [ 0 or more occurrences of ] () parenthesis for grouping / precedence
| RE: a(b | c) RE: a* |
L :{ab,bc} L :{empty,a,aa,aaa,aaaa,aaaaa,…}
| RE: a(b | c)* L:{a,ab,ac,abbc,abccc,…} |
| RE: a(b* | c*) L:{a,ac,accccc,ab,abbb,abb,…} |
| RE: a*(b | c) L:{bcc,ab,aaaab,aaac,…} |
Extended RE:
- one or more -> a+ = aa* ? option; 0 or 1 -> aab? = aa | aab
RE: a+ L:{a,aa,aaa,aaaa,…} NO EMPTY
RE produces a set of strings
The language specified by a regular expression is a regular language
RE generates all elements of a RL
RL is specified by a RE
RL is recognized by a finite state automata
Deterministic finite state automata :: DFA
- deterministic: in every situation, there is no arbitrary choice. If there is a way, only one way finite: yep, finite number of states
L is a regular language if (a) or (b)
- (a) L can be described by a RE, r L consists of only strings generated by r, and no more/less
Even number of a’s followed by any # of b’s
- L{aabb, aab, aabbb}
- RE:
(aa)*bb * | aa(aa)* b* - DFA:
Assignment
Input file: (named inp)
this is a
3 line file < 4 lines
to run 3 + 5 = 8 fun
command to run: % ./a.out < inp
output:
Assume now a few more notational conveniences
Named sets, named RE’s
| D = (0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9) |
| L = (a | b | ….z | A | B | … | Z) |
| C language ID? = L ( L | D | _ )* |
id =
posIntLit = D D* D+
| signedIntLit = -8 +15 34 (+ | -) D+ | D+ |
(+|-)? D+
| FloatLit = +4.5 -3.14 4.5 123.5678645 (+ | -)? D* . D+ |
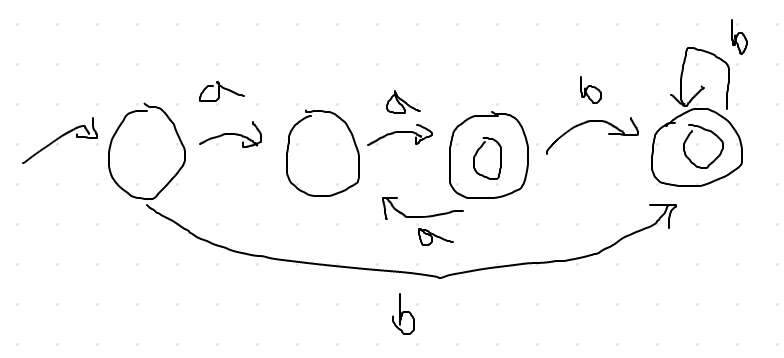
Our goal: a(bc)*d
input: string output: Yes/No accept/reject decision
We are going to use $ to mark end of string rather than dealing with end-of-string & whitespace
ex) abcd$
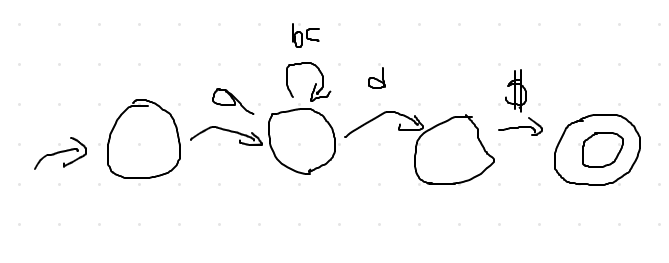
- Hardcode
while(good == 1)
{
switch(s)
{
case 1:
if (c == 'a') t = 2;
else {t = -1; good = 0;}
break;
case 2:
if(c == 'b') t = 3;
else if(c == 'd') t= 4;
else {t = -1; good = 0;}
break;
case 3:
if(c == 'c') t =2;
else {t = -1; good =0;}
break;
case 4:
if(c == '$') {good = 2;}
else {good = 0;}
break;
}
}- Use a table drive DFA-like algorithm
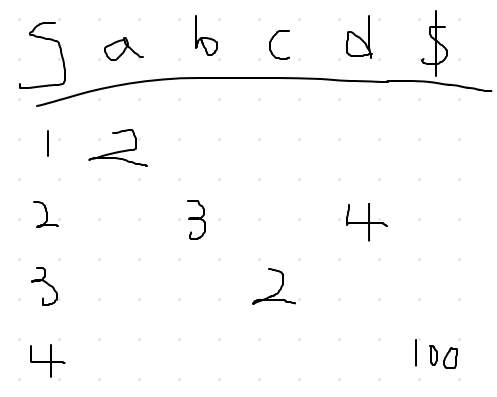
//set-up
tab[1][1] = 2;
tab[2][2] = 3;
tab[2][4] = 4;
tab[3][3] = 2;
tab[4][5] = 100;
scanf("%s", in);
cs = 1;
c = in[0];
loc = 1;
while (cs > 0 && cs < 100)
{
switch(c)
{
case 'a' : c = 1; break;
case 'b' : c = 2; break;
case 'c' : c = 3; break;
case 'd' : c = 4; break;
case '$' : c = 5; break;
}
}a(bc)*d {printf("Accept (%s) \n", yytext);}
xy {printf("Got (%s) \n", yytext);}
.+ {printf("Reject (%s)\n",yytext);}lex inlex.l
gcc lex.yy.c
gcc lex.yy.c -ll
./a.out
- Lex / Flex — Scanner generator
- In:: Regular Expressions
- Out:: Program to implement scanner (automata)
Formal Method + Implementation ==> Hybrid notation
Write the specification
Run spec through Lex
Compile generated generic program + data tables
Run the scanner
Spec.l -> Lex -> Lex.yy.c -> gcc -> Scanner
Exercise
nano file.l (lex file)
definitions & char sets
%%
RE
%%
additional code
lex file.l (generates lex.yy.c)
gcc lex.yy.c -ll (generates a.out scanner)
./a.out < myinfile
Reminders:
- Lex rules – modified RE syntax
-
Lex rules – order matters, matches top to bottom
-- tries to match longest sequence - unmatched characters are echoed by default
- Lex action – when a rule is matches, code fires
- Eventually
-
(0 1 2 3 4 5 6 7 8 9)(0 1 2 3 4 5 6 7 8 9)* -
(0 1 2 3 4 5 6 7 8 9)+ - [0-9]+
- Above three are all same
- . allows everything except ‘\n’
- [a-zA-Z] indicates all alphabetic letters
- [akrz] means only those four characters allowed
-
[a-z A-Z] menas only one character from those letters - Ordering rule is important If you place .+ at first rule, everything will be catched
- If you want to use dot(.), use escape character() so it is like (.)
- ” “” “+ means morethan 2 spaces
-
DT: DataType - Int Char - ID: Identifier - starts & ends with letter
- N : Numeric Literal - positive number
- C : Character literal ‘k’
- ”’”.”’” means covered by small quote(‘)
- a-zA-Z? means starts & ends with letter
- a-zA-Z* same with this?
- Lex is case sensitive
- learn the formal method
- describe a language; generate the elements
- develop a specification
- generate a tool from the spec
topics
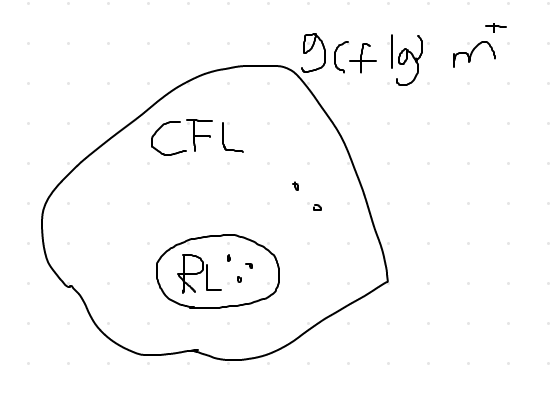
- context free grammar(CFG)
- context free language(CFL)
- derivation
- left-most(LMD)
- right-most(RMD)
- parse tree (PT)
- ambiguity
- abstract syntax tree (AST)
- regular grammar (RG)
- expression example we’ll use all term
YACC - building tools from specification
Parset:
- group chunks together to form constructs
char –> Scanner –> tokens –> Parser –> constructs
Context-Free Grammar (CFG)
- defines a context-free language (CFL)
- just like a RE defines a RL
- Will be used to define the structure of constructs
- Like RE was used for the scanner phase
- Series of rewriting rules
- LHS: single symbol
- RHS: one or more symbols
First some examples; then a more formal coverage
This always backfires when I try to explain or describe something to motivate the new topic. But I keep trying
Person: Bob, Sue, Lisa
Food: noodles, carrots, cookies
What are the option for something of this form??
- person likes to eat food
- Bob likes to eat noodles
- It is same as P(person) likes to eat F(food)
We do have to define where to start, in this case, A
- A = a
- A = a B a
- B = b
-
B = c
- S = g R T
- R = f
- R = g
- T = m T
- T = m
Language: { gfm, ggm, gfmm, ggm, …}
Grammar conventions(for class)
- must have a unique start symbol
- we’ll distinguish
- terminals: lowercase and symbols
- nonterminals: uppercase
- start: the first
- Derivation: from the start symbol,
- series of rewritings steps to arrive at a word(terminal string)
- start at START
- any single nonterminal NT symbol
- start at START
- series of rewritings steps to arrive at a word(terminal string)
- Terminal: lowercase
- Nonterminal: uppercase
Exersise
a+
- S = a
- S = a S
Derivation: aaa
s = a S = a a S = a a a
- S = S a
- S = a
Derivation: aaa
S = S a = S a a = a a a
a+b+
- S = A B
- A = a
- A = a S
- B = b
- B = b S
| (0 | 1)+ |
- S = A
- A = 0
- A = 1
- A = 0 A
-
A = 1 A
- S = 0
- S = 1
- S = 0 S
-
S = 1 S
- S = 0
- S = 1
-
S = S S
- S = S 0
- S = S 1
- S = 0
- S = 1
Derivation : 1 1 0 1(LMD)
- S = SS
- S = 1S
- S = 1SS
- S = 11S
- S = 11SS
- S = 110S
- S = 1101
Ambiguous
Valid C identifier Letters: (a or b) Digits(7 or 8)
| L(L | D)* |
ID = A B ID = A A = a A = b A = A A B = 7 B = 8 B = B B B = A
Exercise2
A sample
- A = a B C d
- B = Bb
- B = x
- C = gh
Context Free Grammar G:
- NT = {A,B,C} T = {a,b,d,g,h,x} S = A
- Rules: production Rules: Rewriting rules:
{ A = a B C d B = Bb B = x C = gh }
L(G) is a context free language
- elements are all strings containing only terminal symbols that can be produced by the grammar
BNF Backus-Naur Form
Grammar rules: LHS non-terminal RHS combination of T & NT
Derivation: starting from the start symbol, apply a valid sequence of rewriting operations to produce the desired string of terminal symbols
- Left-most [given choice, rewrite the left NT first]
-
Right-most[given choice, rewrite the right NT first]
- String with even number of a’s, only a’s, at least 1 a
- (aa)+
- CFG: S = A
- A = aa
- A = aaA
- Derivation: S = A
- S = aaA
- S = aaaa
- IDList
- IDL = id
- IDL = id, IDL
- or
- IDL = id
- IDL = IDL, id
- Positive binary integers, no leading 0’s
- ex) 101; 111000;
-
RE : 1(1 0)* - CFG: S = 1A
- S = 1
- A = 1
- A = 0
- A = AA
- Positive number of a’s followed by same number of b’s
- RE : a+b+
- CFG: S = AB
- A = a
- A = aA
- B = b
- B = bB
- Positive number of a’s followed by b’s (# a’s is bigger than b’s )
- ex) aaaabb
-
RE : a(a b)+b -> I don’t know - CFG: S = aaSb S = aSb S = aaSb S = ab
- CFG: S = aSb S = aAb A = a A = aA
Consider these 3 grammars
- understand
- RMD for aaaa
- PT for aaaa
A = A A A = a
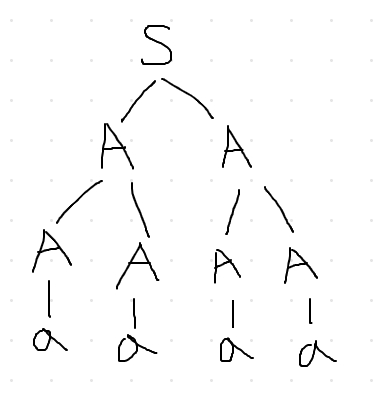
this is wrong
A = A A A = A A A A = A A a A = A a a A = A A a a A = A a a a A = a a a a

this is correct
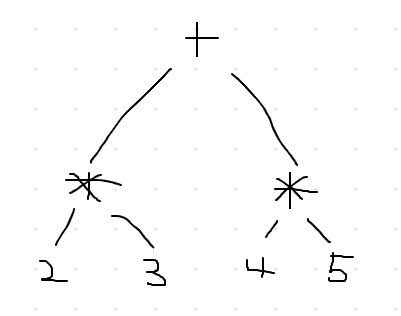
Grammar:
- Expr = Expr + Expr
- Expr = Expr * Expr
- Expr = id
- Expr = num
Derive & draw parse tree
- id + id + id
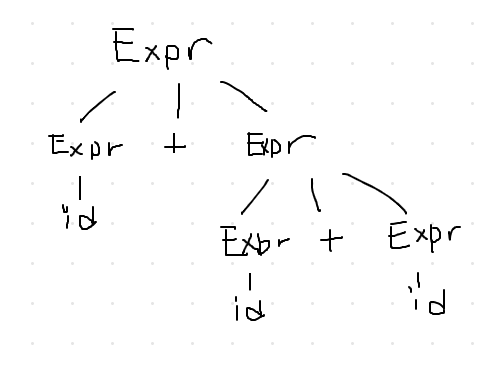
But this is ambiguous grammar
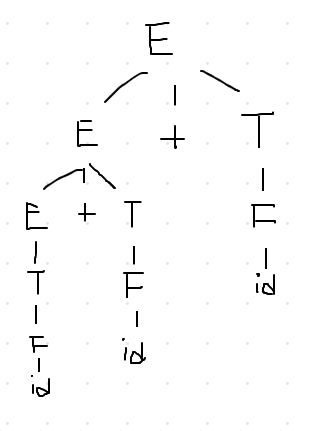
Another Grammar:
- E = E + T
- E = T
- T = T * F
- T = F
- F = id
- F = num
Derive & draw parse tree
- id + id + id
- id + id * id
- id * id + id
Attribute Grammar
What is attribute
- perhaps you’ve heard that word before?
Parse tree
Decorated parse tree - attributes attached to tree - computed based on rules associated with CFG
YACC is based on this formalism, so let’s dig in
Attribute & computation rules are associated with CFG rules
G = A { G.len = A.len } A = a { A.len = 1 } A = a A { A.len = 1 + A1.len }
| { s | s in (a | b)+ and num_s(s)=num_b(s) } |
Let’s work up the attribute grammar
a) Start with CFG [[ note it may not be “the language” ]]
b) Determine attributes
c) Add the rules
d) Test it abb
Do you know how to convert a decimal string to a decimal integer? Reading left to right?
- when we go to next digit, multiply number by 10 and add another digit.
If it is right to left?
- when we go to next digit, multiply next digit by 10^index and add digit.
Binary to int left to right
- complecated
- S = A
- A = 1
- A = 0
- A = 1A
- A = 0A
- Value X 2 + (1 or 0)
- 110 equals 6
- 1101 equals 13
Binary to int right to left
- simple
Synthesized & Inherited - Synthesized : bottom to top - Inherited: top to bottom (or across)
Can do things that are not possible with CFG alone
[b2d.y]
G = B {}
[updown.y]
[Pre2Post] do it together instead of just showing
input: prefix expression
output: postfix expression
Pre : + * 3 4 5
In : 3 * 4 + 5
Post: 3 4 * 5 +
Consider source language:
x := 3 + 4 * 6
[PreTrans] = convert infix to prefix
= keep variable name; use IS for assignment
Part 1
You all do this::
Theme::: [[StackPost]]
output : Postfix stackulator
In: x := 3 + 4
Out: push 3
push 4
add
store x
In: x := 3 + 4 * 5
Out: push 3
push 4
push 5
mul
add
store x
Exam
- Regular grammar can be expressed in Context Free Grammar
- a b+ c is equal abc, abbc, …
- CFG(set of rules) S = aBc, B = bB, B = b
- Parse tree S(a,B(b,B(b)),c)
- Regular grammar S = aB, B = bB, B = bC, C = c S(a,B(b,B(b,C(c))))
- DFA
New Subject
Front-end of the compiler
- scanner & parser
- deal with the source language
- syntax & static semantics
Raw characters –> scanner –> tokens
Static semantics
- things we can check at “compile” time
Dynamic semantics
- things that happen a “run” time
- a little tougher to work with
Symbol Table
- track usage of user-defined names
- add: on declaration
- check: on name usage
Use Lex & Yacc
- validate date & time entries in a file
- for simplicity assume 1 item per line
input
7:23am
3/27/20
8:11pm
output
7 23
27.3.20
20 11
Syntax directed translation
- the source language specification and associated tools drive the translation process action rules on the parser
- Language processing task connected to the rules used to define the syntax (parsing)
And we’ll generate a target image rather than
s0; while(cond) { s1; s2; } s3;
stmt = while (cond) block
$3.code (condition)
$5.code (block)
START x: FLOAT; y: INT; z: FLOAT; w: INT;
x := 2.25;
y := 3;
z := x + y;
w := x + y;
FINISH
START x: INT; y: INT; x: INT; yes: INT; no:BOOL; x:= 5; y:=6.78; yes := x + y ; yes:=x+no; FINISH
START y: FLOAT;
y:= 3.45; y:= FLOAT; FINISH
sscanf(yytext, “%d”, &yylval);
G = G $
G = a B G
G = b
B = f B n
B = h
Recursive-Descent Parser
- Top-down parsing can be viewed as an attempt to find a left-most derivation for an input string