Dice, Cards, and Probabilities
AI Basic Probability
History of probability
1500’s : Girolamo cardano(1501-1576)
- First one to write down math about dice outcomes
- Memtion the important of knowing the # of events that result in a favorable outcome to the # of events that result in an unfavorable outcome.
- Only in this ratio can mutual wagers be laid so that one can contend on equal terms
1600’s : Galileo Galilei(father of modern science, astronomy)
- studied math’s role in gambling and in dice games(1613-1623)
- noted # of different sums that were possible when 2 or 3 dice were used and the number of ways the sums could occur.(cardano had thought about those things but his research was not published until the late 1600’s)
Antoine Gambaud(1607-1684) aka, chevalier de mere
- an accomplished gambler.
- claims he made/questions he asked
- Its profitable to bet with even odds on rolling at least one six in for rolls of a die.
- Its profitable betting on one or more double sixes in 24 rolls of two dice
- How to divide the prize fairly based on present scores. When a contest is only partially completed AKA “The problem of points” was first published in 1494 by Far Luca Paccioli the father of modern accounting
1654 De mere reached out to Blaise Pascal about #2 and #3
- Pascal and fermat wrote letters back and forth and de mere’s questions were finally answered (probability is born)
- This is where probability was thought to have been born, i.e., publicly stated. “Pascal’s triangle and binomial distribution”
Terminology
- Performing an action that results in an outcome by chance is called an experiment. The set of possible outcome from the experiment is called the sample space.
- A subset of a sample space is called on event, for which we are interested in the probability, or chance, that it will happen.
- When probability experiment involves more than one action, we often use a tree diagram or a table to find the sample space.
- The multiplication principle for independent events -> The results of each event does not affect the results of the other
- If action 1 can be performed in n ways and action 2 can be performed in m ways, Then the number of ways of performing action 1 and then action 2 is m*n
De Mere’s 1st question
- We need to calculate the total number of outcomes for rolling 1 die 4 times:
6*6*6*6= 6^4 = 1296 possible outcomes - We want to know how many outcomes involving rolling at least one six. It’s easier to count how many outcomes do not involve rolling a 6.
- There are
5*5*5*5 = 625ways to not roll a single 6 - Thus, there are 1296-625 = 671 possible outcomes for rolling at least one 6.
- The probability of rolling at least one 6 in 4 rolls of a single die is = 671/1296 :: #successful outcomes / total # of outcomes :: .5177 > 1/2
De Mere’s 2nd question
- Its profitable betting on one or more double sixes in 24 rolls of two dice => (36)^24 possible outcomes
- There are (35)^24 possible ways to not rolling double sixes.
- The probability of not rolling double sixes is (35)^24 / (36)^24 :: (35/26)^24 :: 0.5086 > 1/2
- So, the probability of rolling at least once double sixes.
- 1-(35/36)^24 :: 0.2914 < 1/2
Probability Exercise
- Dice Problems



- Card Problems
- 52 cards in a standard deck
- 4 suits: spades,clubs,hearts,diamonds
- 13 cards of each suit
- 4 cards of each: Ace,2,…,10,Jack,Queen,King
We will assume perfect shufflling and honest dealing
When being dealt cards without seeing any of the cards, The probability of being dealt:
- The ace of hearts 1/52
- heart 13/52 = 1/4
- Jack 4/52 = 1/13
When cards are exposed, this affects the probability of drawing the next card as cards are drawn without replacement.
ex) Suppose the first card dealt without replacement is the 4 of clubs. What is the probability that second card dealt is:
- a club 12/51
- a four 3/51
ex) What is the probability of the following:
- getting a 7 or a heart in a single draw
- 4/52 + 12/52 (since we have heart 7)
- If 11 cards have been seen, exactly one of which is a 5, what is the probability of the next being a 5?
- 3/41
- Being dealt a jack and then a second jack in two consecutive cards?
- 4/52*3/51 = 1/221
Roulette, Probability and Odds
P(E) = Probability that event occurs
0 <= P(E) <= 1
P(E) is a decimal or a fraction
P(E) = # of elementary events in E / # of elementary events
P(E) = # of successful outcomes / # of trials
As # of trials goes to infinity, above two P(E) are the same
Odds for E = P(E) / 1 - P(E)
Odds against E = 1 - P(E) / P(E)
They are reciprocal of each other
Typically odds for /against are written as a:b
So,the odds against would be written as b:a
If the odds for E are a:b, then P(E) = a/a+b
- Why? P(E)/1-P(E) :: a/b
- (1-P(E))a = P(E)b
- a-P(E)a = P(E)b
- a = P(E)b+P(E)a
- a = P(E)(b+a)
If the odds against E are a:b, then on a winning bet of $b you get a profit of $a.
So you would get back your wager of $b plus an additional $a.
ex) During the preseason the odds against winning the superbowl were:
Kansas city Chiefs : 8:1
San Francisco 49ers: 16:1
Suppose you had bet $100 during the preseason that KC would win the superbowl and then they do:
8/1 = 8:1 => bet $1 have profit of $8
Same question but Win SF:
36/1 = 36:1 => bet $1 have profit of $36
ex) The KC chiefs currently have 5:6 odds against winning the superbowl. Suppose you bet $100 they win and they do. How much profit would you make on your bet?
5/6 = 5:6 => bet $6 profit is $5
100/6 * 5 => $83.3
ex) What are the odds against drawing a jack from a standard deck?
Odds against = 1-P(E)/P(E)
1-4/52 / 4/52 = 12
The odds against drawing a jack is 12:1
Game Play : Roulette roulette77.us/american-roulette
- Scroll down to read rules first
- Play the game
- What you observed?
- many ways to bet
- True odds and house odds
- ex) if you bet on # 32
- honest calculation = true odds
- 1-P(E) = 1-1/38 / 1/38 = 37:1 (odds against if you bet $1, get $37)
- but house odds: 35:1 (odds against if you bet $1, get $35)
- so house odds are smalling down a little
- Let E = event that a spin of the wheel results in a 10,11,13,or 14. What is the probability of E and the odds for and against E.
- P(E) = 4/38 :: 2/19
- Odds for E = P(E)/1-P(E) :: 2/19 / 1-2/19 :: 2/17 :: 2:17
- If odds for E = a/b, then P(E) = a/a+b implies odds for are 2:17
- Odds against E: 17:2
Compund Probabilities: The rules of the game
- When to disjoint and when it is independent
- Let E and F be events
- The event not E is when E does not occur(complement of E)
- The event E or(inclusive or) F occurs when at least one of E and F occur.
- The additive rule: If E and F are events, then P(EorF)= P(E)+P(F)-P(EandF)
- If E and F are disjoint(they can’t occur simultaneously) events, then P(EorF) = P(E)+P(F)
- ex) a box contains 3 red tickets, 2 blue tickets, and 1 yellow ticket
- If one ticket is drawn randomly from the box, what is the probability it is blue or yellow?
- It is disjoint event (since a ticket can not be both yellow and blue)
- P(blue or yellow) = P(blue) + P(yellow) = 2/6 + 1/6 = 1/2
- Continue
- If two tickets are drawn at random with replacement from the box, what is the probability that the first ticket is blue or the second ticket is yellow?
- Not disjoint
- P(1st blue or 2nd yellow) = P(1st blue)+P(2nd yellow)-P(1st blue and 2nd yellow)
- Draw table first
- 2/6 + 1/6 - (2/36) = 1/2 - 1/18 = 8/18 = 44%
Conditional Probability
-
The Probability of an event E given that we know that event F has occured is called the conditional probability of E given F We denote this by P(E F) -
The multiplication rule: Given events E and F, P(E and F) = P(E)P(F E) and P(F)P(E F) -
If E and F are independent(occurence of one event does not affect the occurence of the other) events, then P(E F) = P(E) and P(F E) = P(F) - So P(E and F) = P(E)P(F)
- Equals P(E) = P(E and F)/P(F)
- Equals P(F) = P(E and F)/P(E)
- ex) A box contains 75 tickets 30 red, 25 blue, 15 yellow, and 5 pink.
- If 3 tickets are drawn from the box at random with replacement what is the probability that all 3 are red?
- P(1st red and 2nd red and 3rd red)
- Events are independent because there is a replacement
- P(30/75 * 30/75 * 30/75)
- P(2/5 * 2/5 * 2/5)
- 8/125 = 6.4%
- If 3 tickets are drawn from the bo at random without replacement, what is the probability that all 3 are red?
- P(1st red and 2nd red and 3rd red)
- Events are dependent because there are no replacement
-
P(1st and 2nd red)*P(3rd red (1st red and 2nd red)) -
P(1st red)*P(2nd red 1st red)*P(3rd red 1st red and 2nd red) - (30/75)(29/74)(28/73) = 6.01%
Real Case (2019 Novel Corona Virus)
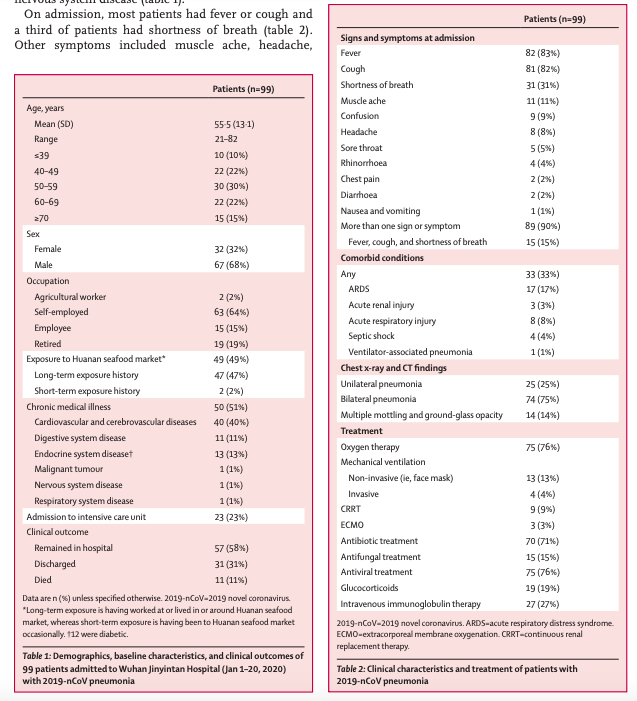
Facts
- If you have chronical medical illness, probability of getting infected is 51%
- If you are male, probability of getting infected is 2 times more than female(32% probability of getting infection)
- If you are younger than 39 years old, probability of getting infected is 10%
- If you have no symptom, probability of getting infected is 10%
Questions
- If you have chronical medical illness and 39 years old male.
- P(medical illness & 39y & male)
-
P(A and B) equals P(A)P(B A) only if A and B are dependent. - Here we have only the fact as independent so P(A) * P(B)
- P(medical illness) * P(39y) * P(male)
- 51/100 * 10/100 * 64/100
- 3.26%
- If you have chronical medical illness and 50 years old female(Alpha). And you met person from wuhan who has no symptom 50y male(Beta).
- P(medical illness & 50Y & female) met P(no symptom & 50 & male)
- This time, meeting people is dependant relationship.
- Let’s say dependant parameter as meeting time
- Spend time 30m or less (30%)
- Spend time 31m to 60m (66%)
- Spend time 61m ~ (88%)
- Alpha P(medical illness) * P(50y) * P(female)
- 51/100 * 90/100 * 32/100
- Beta P(no symptom) * P(male)
- 10/100 * 64/100
- P(14.69%) and P(6.4%)
-
P(14.69%)P(6.4% 66%) [60minutes] - 0.62%
-
P(14.69%)P(6.4% 88%) [90minutes] - 0.83%
Mathemathical Expectation and its Applications
Suppose a friend offers you a friendly bet. If you flip a coin and get heads, they will pay you $1, and if the coin comes up tails, you have to pay them $1. Is this a fair bet?
over time, 1/2 the time you win and 1/2 the time you lose.
We could compute the average winnings (expected value)
(1/2)($1) + (1/2)(-$1) = $0
Average of winning is nothing, but safe game.
Ex) game: tosses to toss a heads
This may take a while so let’s restrict down to three tosses.
Sample space for this game: {H,TH,TTH,TTT}
| Payment table: H | TH | TTH | TTT |
| $1 | $2 | $4 | $0 |
What is a reasonable price to play this game? Probabilities of our outcomes from sample space:
| Outcome | H | TH | TTH | TTT |
| Probability | 1/2 | 1/4 | 1/8 | 1/8 |
Let’s calculate the average expected earnings:
(1/2)$1 + (1/4)$2 + (1/8)$4 + (1/8)$0 = $1.5
So it appears we would be willing to pay $1.50 to play
Math expectation and its applications
- If values W1,W2,…,Wn can be obtained from an experiment with respective probabilities P1,P2,…,Pn, then the expected value of the experiment is given by
Expected value = PiW1+PaW2+…+PnWn
- Find the expected value for the sum when roll a pair of dice
- w1,w2,…,w11 = possible sums that occur(2,3,4,…,12)
- p1,p2,…,p11 = probability that each occurs respectively
- Expected value = (1/36)2+(2/36)3+(3/36)4+(4/36)5+(5/36)6+(6/36)7+(5/36)8+(4/36)9+(3/36)10+(2/36)11+(1/36)*12
- 7: The expected outcome for the sum when rolling 2 dice is 7
EX) For the “first five” wager in Roullette, we need either 0,00,1,2, or 3 to come up. With a payout of 6:1, what are the expected winnings?
- Expected winnings = Succeed[(5/38)($6)]+Lose[(33/38)($1)] :: -$0.0789
- The house has about a 7.89% advantage
- Suppose an urn has 5 blue marbles and 3 red marbles. Assuming the marbles are replaced after being drawn, find the probability that the first two draws consist of one red and one blue marble
P(One red marble and one blue marble)
- This is not first read and second blue
-
P(1st red)P(2nd blue 1st red) + P(1st bue)P(2nd red 1st blue) - If it is independent, P(1st red)P(2nd blue) + P(1st blue)P(2nd red)
- 3/8 * 5/8 + 5/8 * 3/8
Backgammon game
-
Conclusions: If you have to leave a blot within 6 spots of your opponent, leave your blot as close to your opponent as possible. If you can place your blot at least 7 spots away, the further the better (except 11 and 12)
-
Suppose there are two blots, then the probability of hitting at least one of two pieces at distance of 3 and 9 from your piece is?
- P(hitting distance of 3 or hitting the distance of 9)
- P(hitting 3) + P(hitting 9) - P(hitting both)
- 14/36 + 5/36 - 3/36
- 16/36 = 4/9
Entering and Bearing off
- Bearing off: can start once all of your pieces are in your inner table
- Maximize the chance of winning on the following roll.
- ex) your inner table is indicated as follows
- You roll a 2 and a 1.
- Do you move to the 3 and 2 points or the 4 and 1 points?
- Let’s look at 3 and 2 points(Not winning)
- (1,1),(1,2),(1,3),(1,4),(1,5),(1,6),
- (2,1),(3,1),(4,1),(5,1),(6,1)
- we’ve got 11 not winning case : 1-11/36 = 25/36
- Let’s look at 4 and 1 points(Not winning)
- (1,1),(1,2),(1,3),
- (2,1),(3,1),(2,3),(3,2)
- we’ve got 7 not winning case :: 1-7/36 = 29/36
-
Conclusion: we make the more to the 4 and 1 points to have the better chance of winning on the following more.
- Entering innertable, two pieces and probability of finishing it at one turn.
The doubling cube
S = current state
P = your estimated probability of winning the game
1 - P = your estimated probability of losing the game when should you accept a double?
EV(refuse) = expected value = -S EV(accept) = P(2s)+(1-p)(-2s)=2ps-2s+2ps
= 4ps - 2s
= S(4p-2)
EV(accept) > EV(refuese)
S(4p-2) > -S
4p-2 > -1
4p > 1
p > 1/4
- It seems reasonable to accept a double when p > 1/4
When should you ask your opponent to double?
EV(opponent refuses) = S
EV(opponent accepts) = p(2s)+(1-p)(-2s)=s(4p-2)
When is EV(opponent accept) > EV(opponent refuse)?
S(4p-2) > s
4p-2 > 1
4p > 3
p > 3/4
If p < 3/4 you would prefer a concession and if p > 3/4 you hope they accept your doubling
EV(no double is offered) = P(s) + (1-p)(-s) = s(2p-1)
EV(no double) = EV(opponent accepts)
s(2p-1) = s(4p-2)
2p-1 = 4p-2
1/2 = p
Conclusion: when p > 1/2 doubling seems reasonable and when p > 3/4 you hope your doubling gets a accepted.
You are white and the board is a shown It is your roll and you control the doubling cube. Should you double?